OPPOSITE VECTORS

In the field of physics , vectors are quantities that are defined by their quantity, their direction, their point of application and their meaning. Vectors can be classified in different ways according to their characteristics and the context in which they act.

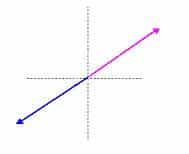
Opposite vectors are known as those that have the same direction and the same magnitude , but have opposite directions . According to other definitions, the opposite vectors have the same magnitude but opposite direction because the direction also indicates the direction.

The idea of opposite vectors, in short, implies working with two vectors that have the same magnitude (that is, the same module) and the same direction, although with the opposite sense. It can be said that a vector is opposite to another when it has the same magnitude but appears at 180º . In this way, the vector is not only opposite to the other, but it is also its negative .

Let us take the case of the vector RS and the vector MN . The coordinates of the vector RS are (4,8) , while the coordinates of the vector MN are (-4, -8) . Both vectors are opposite vectors: vector MN is the negative vector of vector RS . In a graphic representation, it would be clear how both vectors have the same module (they would occupy the same space in the diagram) but in the opposite direction.

It is important to note that if we add two opposite vectors we will obtain a null vector as a result , also known as a zero vector since its module is equal to 0 (it has no extension).

The graphic representation of vectors always helps us to understand their characteristics more clearly, and in the case of opposites this is also true, partly thanks to the inclusion of another concept: the cardinal points. If we leave aside for a moment the components (or terms) of the vector, which we can define as their values ​​in each Cartesian axis, and we simply focus on its module and the angle it forms with the X axis , then we can say that the vector 25 meters with an angle of 50 ° to the North of the West is opposite the 25 meters with an angle of 50 ° to the South of the East.

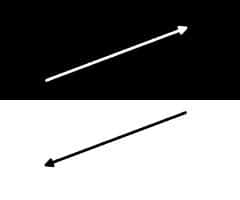How can we represent such a pair of opposite vectors on a graph? First, note that we are dealing with two - dimensional vectors, as we have just provided information to two respective axes , which are usually identified with the letters X and Y . Therefore, the first step is to draw the two axes.

Next, we must consider for a second the location of each "hemisphere" within the space that we have just traced: we can say that the Northwest is in the upper left quadrant. As the last step of this preliminary preparation stage, it is necessary to establish a scale , to know how much the 25 meters will be equal on our sheet. Then, it only remains to draw the two vectors. To do this, we must remember that the angle is formed with respect to the X axis , that is, the horizontal.

With the help of a protractor, we must determine the point through which the first vector must pass, which will have its origin at (0,0), that is, at the vertex of the Cartesian axes. Taking into account the aforementioned scale, we draw a line of the relevant measure and, voila. To respect the conventions and make our graph easy to read by other people, it is recommended to draw two small lines at the top of the vector as an "arrowhead", as well as to indicate the internal angle with a curved line.

Having the main vector, drawing its opposite is much easier, since it is not necessary to calculate the angle or its length again, but simply align a ruler to the first and draw it towards the Southeast (the lower right quadrant) with the same extension .