CONCURRENT VECTORS

Vector is a concept with several uses. In this case, we are interested in its meaning in the field of physics , which indicates that a vector is a quantity defined by its value, its sense, its direction and its point of application. Concurrent , on the other hand, is that which concurs (that is, that meets or coincides with something else).

Vectors can be classified differently according to their characteristics . It is called concurrent vectors those traverse the same point . Due to the fact that, when passing through this point, an angle is created, the concurrent vectors are also called angular vectors.

Suppose that two helicopters take off from the same point . One of the aircraft is heading east and the other is heading west. Both helicopters carry out a route that can be represented with a vector; as they have the same point of application, they are concurrent vectors.

Take the case of an architect who draws the window of a room. In the plane , to represent the window, takes a rectangle with four vectors: A , B , C and D . According to the above, we can say that A and B , B and C , C and D , and D and A are concurrent vectors, since they intersect. However, A and C are not concurrent vectors, nor are B and D .

One of the aspects that makes vectors so particular within the field of physics is that they not only represent an isolated value, but also combine a length with an orientation , and it is thanks to this that they are such versatile tools, with so many applications in different fields.

As can be deduced from the previous paragraphs, vectors can be used in both two-dimensional and three-dimensional spaces, and it is in the latter that we find them most often: the examples above show a case in three dimensions (helicopters) and another in two. (window).

Making use of the aforementioned versatility of vectors and their many fields of application, let's think of an example that complements the previous two. In this case, they will not represent the movement of a vehicle or a series of segments drawn to find a suitable design: they will be two or more strings that pull an object, from the same point.

If we tie a rope around a heavy box and let its two ends emerge from the knot, we will be able to share its weight with another person, since each one will be able to pull one of them. In this case, the concurrent vectors clearly show us the concept of vector sum , since even though there are two different orientations and forces, the box will only move in one direction .

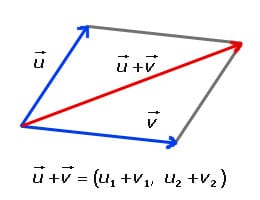In the second image, it can be seen that from the same starting point of the two concurrent vectors drawn in red, a third arises, concurrent to both, which indicates the direction in which the object tied with the rope and pulled by two people would move.

The formula to calculate the value of this new vector is also in the image: you simply have to add the corresponding components .

To represent the sum graphically, it is possible to use the parallelogram method : it consists of drawing two lines, each one parallel to one of the vectors and the other passing through the end, so that when they cross they intersect at a point that serves to close the figure. This point will be the end of the new vector.

Beyond the concurrent vectors, other types of vectors are unit vectors , the collinear vectors , the coplanar vectors , the vectors parallel and opposite vectors .